Portal:Mathematics

Abacus, a ancient hand-operated calculating.
Portrait of Emmy Noether, around 1900.
Euler's identity

Mathematics is a field of study that discovers and organizes methods, theories and theorems that are developed and proved for the needs of empirical sciences and mathematics itself. There are many areas of mathematics, which include number theory (the study of numbers), algebra (the study of formulas and related structures), geometry (the study of shapes and spaces that contain them), analysis (the study of continuous changes), and set theory (presently used as a foundation for all mathematics). (Full article...)

Featured articles

Image 1

Hilary Putnam

The Quine–Putnam indispensability argument is an argument in the philosophy of mathematics for the existence of abstract mathematical objects such as numbers and sets, a position known as mathematical platonism. It was named after the philosophers Willard Van Orman Quine and Hilary Putnam, and is one of the most important arguments in the philosophy of mathematics.

Although elements of the indispensability argument may have originated with thinkers such as Gottlob Frege and Kurt Gödel, Quine's development of the argument was unique for introducing to it a number of his philosophical positions such as naturalism, confirmational holism, and the criterion of ontological commitment. Putnam gave Quine's argument its first detailed formulation in his 1971 book Philosophy of Logic. He later came to disagree with various aspects of Quine's thinking, however, and formulated his own indispensability argument based on the no miracles argument in the philosophy of science. A standard form of the argument in contemporary philosophy is credited to Mark Colyvan; whilst being influenced by both Quine and Putnam, it differs in important ways from their formulations. It is presented in the Stanford Encyclopedia of Philosophy: (Full article...)
Image 2

Damage from Hurricane Katrina in 2005. Actuaries need to estimate long-term levels of such damage in order to accurately price property insurance, set appropriate reserves, and design appropriate reinsurance and capital management strategies.

An actuary is a professional with advanced mathematical skills who deals with the measurement and management of risk and uncertainty. These risks can affect both sides of the balance sheet and require asset management, liability management, and valuation skills. Actuaries provide assessments of financial security systems, with a focus on their complexity, their mathematics, and their mechanisms. The name of the corresponding academic discipline is actuarial science.

While the concept of insurance dates to antiquity, the concepts needed to scientifically measure and mitigate risks have their origins in the 17th century studies of probability and annuities. Actuaries of the 21st century require analytical skills, business knowledge, and an understanding of human behavior and information systems to design programs that manage risk, by determining if the implementation of strategies proposed for mitigating potential risks, does not exceed the expected cost of those risks actualized. The steps needed to become an actuary, including education and licensing, are specific to a given country, with various additional requirements applied by regional administrative units; however, almost all processes impart universal principles of risk assessment, statistical analysis, and risk mitigation, involving rigorously structured training and examination schedules, taking many years to complete. (Full article...)
Image 3

Portrait by Jakob Emanuel Handmann, 1753

Leonhard Euler (/ˈɔɪlər/ OY-lər; German: [ˈleːɔnhaʁt ˈʔɔʏlɐ] , Swiss Standard German: [ˈleɔnhard ˈɔʏlər]; 15 April 1707 – 18 September 1783) was a Swiss polymath who was active as a mathematician, physicist, astronomer, logician, geographer, and engineer. He founded the studies of graph theory and topology and made influential discoveries in many other branches of mathematics, such as analytic number theory, complex analysis, and infinitesimal calculus. He also introduced much of modern mathematical terminology and notation, including the notion of a mathematical function. He is known for his work in mechanics, fluid dynamics, optics, astronomy, and music theory. Euler has been called a "universal genius" who "was fully equipped with almost unlimited powers of imagination, intellectual gifts and extraordinary memory". He spent most of his adult life in Saint Petersburg, Russia, and in Berlin, then the capital of Prussia.

Euler is credited for popularizing the Greek letter π {\displaystyle \pi } (lowercase pi) to denote the ratio of a circle's circumference to its diameter, as well as first using the notation f ( x ) {\displaystyle f(x)} for the value of a function, the letter i {\displaystyle i} to express the imaginary unit − 1 {\displaystyle {\sqrt {-1}}} , the Greek letter Σ {\displaystyle \Sigma } (capital sigma) to express summations, the Greek letter Δ {\displaystyle \Delta } (capital delta) for finite differences, and lowercase letters to represent the sides of a triangle while representing the angles as capital letters. He gave the current definition of the constant e {\displaystyle e} , the base of the natural logarithm, now known as Euler's number. Euler made contributions to applied mathematics and engineering, such as his study of ships which helped navigation, his three volumes on optics contributed to the design of microscopes and telescopes, and he studied the bending of beams and the critical load of columns. (Full article...)
Image 4

Elementary algebra studies which values solve equations formed using arithmetical operations.

Algebra is the branch of mathematics that studies certain abstract systems, known as algebraic structures, and the manipulation of expressions within those systems. It is a generalization of arithmetic that introduces variables and algebraic operations other than the standard arithmetic operations, such as addition and multiplication.

Elementary algebra is the main form of algebra taught in schools. It examines mathematical statements using variables for unspecified values and seeks to determine for which values the statements are true. To do so, it uses different methods of transforming equations to isolate variables. Linear algebra is a closely related field that investigates linear equations and combinations of them called systems of linear equations. It provides methods to find the values that solve all equations in the system at the same time, and to study the set of these solutions. (Full article...)
Image 5

One of Molyneux's celestial globes, which is displayed in Middle Temple Library – from the frontispiece of the Hakluyt Society's 1889 reprint of A Learned Treatise of Globes, both Cœlestiall and Terrestriall, one of the English editions of Robert Hues' Latin work Tractatus de Globis (1594)

Emery Molyneux (/ˈɛməri ˈmɒlɪnoʊ/ EM-ər-ee MOL-in-oh; died June 1598) was an English Elizabethan maker of globes, mathematical instruments and ordnance. His terrestrial and celestial globes, first published in 1592, were the first to be made in England and the first to be made by an Englishman.

Molyneux was known as a mathematician and maker of mathematical instruments such as compasses and hourglasses. He became acquainted with many prominent men of the day, including the writer Richard Hakluyt and the mathematicians Robert Hues and Edward Wright. He also knew the explorers Thomas Cavendish, Francis Drake, Walter Raleigh and John Davis. Davis probably introduced Molyneux to his own patron, the London merchant William Sanderson, who largely financed the construction of the globes. When completed, the globes were presented to Elizabeth I. Larger globes were acquired by royalty, noblemen and academic institutions, while smaller ones were purchased as practical navigation aids for sailors and students. The globes were the first to be made in such a way that they were unaffected by the humidity at sea, and they came into general use on ships. (Full article...)
Image 6

Bust of Shen at the Beijing Ancient Observatory

Shen Kuo (Chinese: 沈括; 1031–1095) or Shen Gua, courtesy name Cunzhong (存中) and pseudonym Mengqi (now usually given as Mengxi) Weng (夢溪翁), was a Chinese polymath, scientist, and statesman of the Song dynasty (960–1279). Shen was a master in many fields of study including mathematics, optics, and horology. In his career as a civil servant, he became a finance minister, governmental state inspector, head official for the Bureau of Astronomy in the Song court, Assistant Minister of Imperial Hospitality, and also served as an academic chancellor. At court his political allegiance was to the Reformist faction known as the New Policies Group, headed by Chancellor Wang Anshi (1021–1085).

In his Dream Pool Essays or Dream Torrent Essays (夢溪筆談; Mengxi Bitan) of 1088, Shen was the first to describe the magnetic needle compass, which would be used for navigation (first described in Europe by Alexander Neckam in 1187). Shen discovered the concept of true north in terms of magnetic declination towards the north pole, with experimentation of suspended magnetic needles and "the improved meridian determined by Shen's [astronomical] measurement of the distance between the pole star and true north". This was the decisive step in human history to make compasses more useful for navigation, and may have been a concept unknown in Europe for another four hundred years (evidence of German sundials made circa 1450 show markings similar to Chinese geomancers' compasses in regard to declination). (Full article...)
Image 7

Portrait by August Köhler, c. 1910, after 1627 original

Johannes Kepler (/ˈkɛplər/; German: [joˈhanəs ˈkɛplɐ, -nɛs -] ; 27 December 1571 – 15 November 1630) was a German astronomer, mathematician, astrologer, natural philosopher and writer on music. He is a key figure in the 17th-century Scientific Revolution, best known for his laws of planetary motion, and his books Astronomia nova, Harmonice Mundi, and Epitome Astronomiae Copernicanae, influencing among others Isaac Newton, providing one of the foundations for his theory of universal gravitation. The variety and impact of his work made Kepler one of the founders and fathers of modern astronomy, the scientific method, natural and modern science. He has been described as the "father of science fiction" for his novel Somnium.

Kepler was a mathematics teacher at a seminary school in Graz, where he became an associate of Prince Hans Ulrich von Eggenberg. Later he became an assistant to the astronomer Tycho Brahe in Prague, and eventually the imperial mathematician to Emperor Rudolf II and his two successors Matthias and Ferdinand II. He also taught mathematics in Linz, and was an adviser to General Wallenstein.
Additionally, he did fundamental work in the field of optics, being named the father of modern optics, in particular for his Astronomiae pars optica. He also invented an improved version of the refracting telescope, the Keplerian telescope, which became the foundation of the modern refracting telescope, while also improving on the telescope design by Galileo Galilei, who mentioned Kepler's discoveries in his work. He is also known for postulating the Kepler conjecture. (Full article...)
Image 8
Logic studies valid forms of inference like modus ponens.

Logic is the study of correct reasoning. It includes both formal and informal logic. Formal logic is the study of deductively valid inferences or logical truths. It examines how conclusions follow from premises based on the structure of arguments alone, independent of their topic and content. Informal logic is associated with informal fallacies, critical thinking, and argumentation theory. Informal logic examines arguments expressed in natural language whereas formal logic uses formal language. When used as a countable noun, the term "a logic" refers to a specific logical formal system that articulates a proof system. Logic plays a central role in many fields, such as philosophy, mathematics, computer science, and linguistics.

Logic studies arguments, which consist of a set of premises that leads to a conclusion. An example is the argument from the premises "it's Sunday" and "if it's Sunday then I don't have to work" leading to the conclusion "I don't have to work". Premises and conclusions express propositions or claims that can be true or false. An important feature of propositions is their internal structure. For example, complex propositions are made up of simpler propositions linked by logical vocabulary like $\land$ (and) or $\to$ (if...then). Simple propositions also have parts, like "Sunday" or "work" in the example. The truth of a proposition usually depends on the meanings of all of its parts. However, this is not the case for logically true propositions. They are true only because of their logical structure independent of the specific meanings of the individual parts. (Full article...)
Image 9
The manipulations of the Rubik's Cube form the Rubik's Cube group.

In mathematics, a group is a set with an operation that satisfies the following constraints: the operation is associative, it has an identity element, and every element of the set has an inverse element.

Many mathematical structures are groups endowed with other properties. For example, the integers with the addition operation form an infinite group, which is generated by a single element called ⁠ $1$ ⁠ (these properties characterize the integers in a unique way). (Full article...)
$Image 10 Euclid's method for finding the greatest common divisor (GCD) of two starting lengths BA and DC, both defined to be multiples of a common "unit" length. The length DC being shorter, it is used to "measure" BA, but only once because the remainder EA is less than DC. EA now measures (twice) the shorter length DC, with remainder FC shorter than EA. Then FC measures (three times) length EA. Because there is no remainder, the process ends with FC being the GCD. On the right Nicomachus's example with numbers 49 and 21 resulting in their GCD of 7 (derived from Heath 1908:300). In mathematics, the Euclidean algorithm, or Euclid's algorithm, is an efficient method for computing the greatest common divisor (GCD) of two integers, the largest number that divides them both without a remainder. It is named after the ancient Greek mathematician Euclid, who first described it in his Elements (c. 300 BC). It is an example of an algorithm, a step-by-step procedure for performing a calculation according to well-defined rules, and is one of the oldest algorithms in common use. It can be used to reduce fractions to their simplest form, and is a part of many other number-theoretic and cryptographic calculations. The Euclidean algorithm is based on the principle that the greatest common divisor of two numbers does not change if the larger number is replaced by its difference with the smaller number. For example, 21 is the GCD of 252 and 105 (as 252 = 21 × 12 and 105 = 21 × 5), and the same number 21 is also the GCD of 105 and 252 − 105 = 147. Since this replacement reduces the larger of the two numbers, repeating this process gives successively smaller pairs of numbers until the two numbers become equal. When that occurs, that number is the GCD of the original two numbers. By reversing the steps or using the extended Euclidean algorithm, the GCD can be expressed as a linear combination of the two original numbers, that is the sum of the two numbers, each multiplied by an integer (for example, 21 = 5 × 105 + (−2) × 252). The fact that the GCD can always be expressed in this way is known as Bézout's identity. (Full article...)$

Image 10
Euclid's method for finding the greatest common divisor (GCD) of two starting lengths BA and DC, both defined to be multiples of a common "unit" length. The length DC being shorter, it is used to "measure" BA, but only once because the remainder EA is less than DC. EA now measures (twice) the shorter length DC, with remainder FC shorter than EA. Then FC measures (three times) length EA. Because there is no remainder, the process ends with FC being the GCD. On the right Nicomachus's example with numbers 49 and 21 resulting in their GCD of 7 (derived from Heath 1908:300).

In mathematics, the Euclidean algorithm, or Euclid's algorithm, is an efficient method for computing the greatest common divisor (GCD) of two integers, the largest number that divides them both without a remainder. It is named after the ancient Greek mathematician Euclid, who first described it in his Elements (c. 300 BC).
It is an example of an algorithm, a step-by-step procedure for performing a calculation according to well-defined rules,
and is one of the oldest algorithms in common use. It can be used to reduce fractions to their simplest form, and is a part of many other number-theoretic and cryptographic calculations.

The Euclidean algorithm is based on the principle that the greatest common divisor of two numbers does not change if the larger number is replaced by its difference with the smaller number. For example, $21$ is the GCD of $252$ and $105$ (as $252 = 21 \times 12$ and $105 = 21 \times 5)$ , and the same number $21$ is also the GCD of $105$ and $252 - 105 = 147$ . Since this replacement reduces the larger of the two numbers, repeating this process gives successively smaller pairs of numbers until the two numbers become equal. When that occurs, that number is the GCD of the original two numbers. By reversing the steps or using the extended Euclidean algorithm, the GCD can be expressed as a linear combination of the two original numbers, that is the sum of the two numbers, each multiplied by an integer (for example, $21 = 5 \times 105 + (-2) \times 252$ ). The fact that the GCD can always be expressed in this way is known as Bézout's identity. (Full article...)
Image 11
General relativity, also known as the general theory of relativity, and as Einstein's theory of gravity, is the geometric theory of gravitation published by Albert Einstein in 1915 and is the current description of gravitation in modern physics. General relativity generalizes special relativity and refines Newton's law of universal gravitation, providing a unified description of gravity as a geometric property of space and time, or four-dimensional spacetime. In particular, the curvature of spacetime is directly related to the energy and momentum of whatever is
present matter and radiation. The relation is specified by the Einstein field equations, a system of second-order partial differential equations.

Newton's law of universal gravitation, which describes classical gravity, can be seen as a prediction of general relativity for the almost flat spacetime geometry around stationary mass distributions. Some predictions of general relativity, however, are beyond Newton's law of universal gravitation in classical physics. These predictions concern the passage of time, the geometry of space, the motion of bodies in free fall, and the propagation of light, and include gravitational time dilation, gravitational lensing, the gravitational redshift of light, the Shapiro time delay and singularities/black holes. So far, all tests of general relativity have been shown to be in agreement with the theory. The time-dependent solutions of general relativity enable us to talk about the history of the universe and have provided the modern framework for cosmology, thus leading to the discovery of the Big Bang and cosmic microwave background radiation. Despite the introduction of a number of alternative theories, general relativity continues to be the simplest theory consistent with experimental data. (Full article...)
Image 12

Noether c. 1900–1910

Amalie Emmy Noether (US: /ˈnʌtər/, UK: /ˈnɜːtə/; German: [ˈnøːtɐ]; 23 March 1882 – 14 April 1935) was a German mathematician who made many important contributions to abstract algebra. She also proved Noether's first and second theorems, which are fundamental in mathematical physics. Noether was described by Pavel Alexandrov, Albert Einstein, Jean Dieudonné, Hermann Weyl and Norbert Wiener as the most important woman in the history of mathematics. As one of the leading mathematicians of her time, she developed theories of rings, fields, and algebras. In physics, Noether's theorem explains the connection between symmetry and conservation laws.

Noether was born to a Jewish family in the Franconian town of Erlangen; her father was the mathematician Max Noether. She originally planned to teach French and English after passing the required examinations but instead studied mathematics at the University of Erlangen, where her father lectured. After completing her doctorate in 1907 under the supervision of Paul Gordan, she worked at the Mathematical Institute of Erlangen without pay for seven years. At the time, women were largely excluded from academic positions. In 1915, she was invited by David Hilbert and Felix Klein to join the mathematics department at the University of Göttingen, a world-renowned center of mathematical research. The philosophical faculty objected, however, and she spent four years lecturing under Hilbert's name. Her habilitation was approved in 1919, allowing her to obtain the rank of Privatdozent. (Full article...)
Image 13

Rejewski, c. 1932

Marian Adam Rejewski (Polish: [ˈmarjan rɛˈjɛfskʲi] ; 16 August 1905 – 13 February 1980) was a Polish mathematician and cryptologist who in late 1932 reconstructed the sight-unseen German military Enigma cipher machine, aided by limited documents obtained by French military intelligence.

Over the next nearly seven years, Rejewski and fellow mathematician-cryptologists Jerzy Różycki and Henryk Zygalski, working at the Polish General Staff's Cipher Bureau, developed techniques and equipment for decrypting the Enigma ciphers, even as the Germans introduced modifications to their Enigma machines and encryption procedures. Rejewski's contributions included the cryptologic card catalog and the cryptologic bomb. (Full article...)
Image 14
The first 15,000 partial sums of 0 + 1 − 2 + 3 − 4 + ... The graph is situated with positive integers to the right and negative integers to the left.

In mathematics, 1 − 2 + 3 − 4 + ··· is an infinite series whose terms are the successive positive integers, given alternating signs. Using sigma summation notation the sum of the first m terms of the series can be expressed as
$\sum _{n=1}^{m}n(-1)^{n-1}.$

The infinite series diverges, meaning that its sequence of partial sums, (1, −1, 2, −2, 3, ...), does not tend towards any finite limit. Nonetheless, in the mid-18th century, Leonhard Euler wrote what he admitted to be a paradoxical equation:
$1-2+3-4+\cdots ={\frac {1}{4}}.$ (Full article...)
Image 15

Cantor, c. 1910

Georg Ferdinand Ludwig Philipp Cantor (/ˈkæntɔːr/ KAN-tor; German: [ˈɡeːɔʁk ˈfɛʁdinant ˈluːtvɪç ˈfiːlɪp ˈkantoːɐ̯]; 3 March [O.S. 19 February] 1845 – 6 January 1918) was a mathematician who played a pivotal role in the creation of set theory, which has become a fundamental theory in mathematics. Cantor established the importance of one-to-one correspondence between the members of two sets, defined infinite and well-ordered sets, and proved that the real numbers are more numerous than the natural numbers. Cantor's method of proof of this theorem implies the existence of an infinity of infinities. He defined the cardinal and ordinal numbers and their arithmetic. Cantor's work is of great philosophical interest, a fact he was well aware of.

Originally, Cantor's theory of transfinite numbers was regarded as counter-intuitive – even shocking. This caused it to encounter resistance from mathematical contemporaries such as Leopold Kronecker and Henri Poincaré and later from Hermann Weyl and L. E. J. Brouwer, while Ludwig Wittgenstein raised philosophical objections; see Controversy over Cantor's theory. Cantor, a devout Lutheran Christian, believed the theory had been communicated to him by God. Some Christian theologians (particularly neo-Scholastics) saw Cantor's work as a challenge to the uniqueness of the absolute infinity in the nature of God – on one occasion equating the theory of transfinite numbers with pantheism – a proposition that Cantor vigorously rejected. Not all theologians were against Cantor's theory; prominent neo-scholastic philosopher Constantin Gutberlet was in favor of it and Cardinal Johann Baptist Franzelin accepted it as a valid theory (after Cantor made some important clarifications). (Full article...)

Good articles

Image 1
Aderemi Oluyomi Kuku (20 March 1941 – 13 February 2022) was a Nigerian mathematician and academic, known for his contributions to the fields of algebraic K-theory and non-commutative geometry. Born in Ijebu-Ode, Ogun State, Nigeria, Kuku began his academic journey at Makerere University College and the University of Ibadan, where he earned his B.Sc. in Mathematics, followed by his M.Sc. and Ph.D. under Joshua Leslie and Hyman Bass. His doctoral research focused on the Whitehead group of p-adic integral group-rings of finite p-groups. Kuku held positions as a lecturer and professor at various Nigerian universities, including the University of Ife and the University of Ibadan, where he served as Head of the Department of Mathematics and Dean of the Postgraduate School. His research involved developing methods for computing higher K-theory of non-commutative rings and articulating higher algebraic K-theory in the language of Mackey functors. His work on equivariant higher algebraic K-theory and its generalisations impacted the field.

During his career, Kuku was elected a Fellow of the African Academy of Sciences, the Nigerian Academy of Science, and the American Mathematical Society. He also received the Nigerian National Order of Merit and the Officer of the Order of the Niger. He served as president of the African Mathematical Union, where he worked to promote mathematics across Africa. Kuku's work extended beyond research, encompassing education and mentorship. He authored several books and articles, supervised graduate students, and fostered international collaborations. (Full article...)
Image 2

In mathematics, the Pythagorean theorem or Pythagoras' theorem is a fundamental relation in Euclidean geometry between the three sides of a right triangle. It states that the area of the square whose side is the hypotenuse (the side opposite the right angle) is equal to the sum of the areas of the squares on the other two sides.

The theorem can be written as an equation relating the lengths of the sides $a$ , $b$ and the hypotenuse $c$ , sometimes called the Pythagorean equation:
: $a^{2}+b^{2}=c^{2}.$
The theorem is named for the Greek philosopher Pythagoras, born around 570 BC. The theorem has been proved numerous times by many different methods – possibly the most for any mathematical theorem. The proofs are diverse, including both geometric proofs and algebraic proofs, with some dating back thousands of years. (Full article...)
Image 3

Einstein in 1921

Albert Einstein (/ˈaɪnstaɪn/, EYEN-styne; German: [ˈalbɛʁt ˈʔaɪnʃtaɪn] ; 14 March 1879 – 18 April 1955) was a German-born theoretical physicist who is best known for developing the theory of relativity. Einstein also made important contributions to quantum mechanics. His mass–energy equivalence formula E = mc2, which arises from special relativity, has been called "the world's most famous equation". He received the 1921 Nobel Prize in Physics for his services to theoretical physics, and especially for his discovery of the law of the photoelectric effect.

Born in the German Empire, Einstein moved to Switzerland in 1895, forsaking his German citizenship the following year. In 1897, at the age of seventeen, he enrolled in the mathematics and physics teaching diploma program at the Swiss Federal Polytechnic School in Zurich, graduating in 1900. He acquired Swiss citizenship a year later and afterwards secured a permanent position at the Swiss Patent Office in Bern. In 1905, he submitted a successful PhD dissertation to the University of Zurich. In 1914, he moved to Berlin to join the Prussian Academy of Sciences and the Humboldt University of Berlin, becoming director of the Kaiser Wilhelm Institute for Physics. In 1933, while Einstein was visiting the United States, Adolf Hitler came to power in Germany. Horrified by the Nazi persecution of his fellow Jews, he decided to remain in the US, and was granted American citizenship in 1940. On the eve of World War II, he endorsed a letter to President Franklin D. Roosevelt alerting him to the potential German nuclear weapons program and recommending that the US begin similar research. (Full article...)
Image 4
The Laves graph

In geometry and crystallography, the Laves graph is an infinite and highly symmetric system of points and line segments in three-dimensional Euclidean space, forming a periodic graph. Three equal-length segments meet at 120° angles at each point, and all cycles use ten or more segments. It is the shortest possible triply periodic graph, relative to the volume of its fundamental domain. One arrangement of the Laves graph uses one out of every eight of the points in the integer lattice as its points, and connects all pairs of these points that are nearest neighbors, at distance ${\sqrt {2}}$ . It can also be defined, divorced from its geometry, as an abstract undirected graph, a covering graph of the complete graph on four vertices.
H. S. M. Coxeter (1955) named this graph after Fritz Laves, who first wrote about it as a crystal structure in 1932. It has also been called the K₄ crystal, (10,3)-a network, diamond twin, triamond, and the srs net. The regions of space nearest each vertex of the graph are congruent 17-sided polyhedra that tile space. Its edges lie on diagonals of the regular skew polyhedron, a surface with six squares meeting at each integer point of space. (Full article...)
Image 5
An $m \times n$ matrix: the $m$ rows are horizontal and the $n$ columns are vertical. Each element of a matrix is often denoted by a variable with two subscripts. For example, $a 2,1$ represents the element at the second row and first column of the matrix.

In mathematics, a matrix (pl.: matrices) is a rectangular array or table of numbers, symbols, or expressions, with elements or entries arranged in rows and columns, which is used to represent a mathematical object or property of such an object.

For example,
${\begin{bmatrix}1&9&-13\\20&5&-6\end{bmatrix}}$
is a matrix with two rows and three columns. This is often referred to as a "two-by-three matrix", a " $2\times 3$ matrix", or a matrix of dimension $2\times 3$ . (Full article...)
Image 6
A set of 20 points in a 10 × 10 grid, with no three points in a line.

The no-three-in-line problem in discrete geometry asks how many points can be placed in the $n\times n$ grid so that no three points lie on the same line. The problem concerns lines of all slopes, not only those aligned with the grid. It was introduced by Henry Dudeney in 1900. Brass, Moser, and Pach call it "one of the oldest and most extensively studied geometric questions concerning lattice points".

At most $2n$ points can be placed, because $2n+1$ points in a grid would include a row of three or more points, by the pigeonhole principle. Although the problem can be solved with $2n$ points for every $n$ up to $46$ , it is conjectured that fewer than $2n$ points can be placed in grids of large size. Known methods can place linearly many points in grids of arbitrary size, but the best of these methods place slightly fewer than $1.5n$ points, not $2n$ . (Full article...)
Image 7
A Hasse diagram of divisibility relationships among the regular numbers up to 400. The vertical scale is logarithmic.

Regular numbers are numbers that evenly divide powers of 60 (or, equivalently, powers of 30). Equivalently, they are the numbers whose only prime divisors are 2, 3, and 5. As an example, 60² = 3600 = 48 × 75, so as divisors of a power of 60 both 48 and 75 are regular.

These numbers arise in several areas of mathematics and its applications, and have different names coming from their different areas of study.
- In number theory, these numbers are called 5-smooth, because they can be characterized as having only 2, 3, or 5 as their prime factors. This is a specific case of the more general $k$ -smooth numbers, the numbers that have no prime factor greater than $k$ .* In the study of Babylonian mathematics, the divisors of powers of 60 are called regular numbers or regular sexagesimal numbers, and are of great importance in this area because of the sexagesimal (base 60) number system that the Babylonians used for writing their numbers, and that was central to Babylonian mathematics.
- In music theory, regular numbers occur in the ratios of tones in five-limit just intonation. In connection with music theory and related theories of architecture, these numbers have been called the harmonic whole numbers.
- In computer science, regular numbers are often called Hamming numbers, after Richard Hamming, who proposed the problem of finding computer algorithms for generating these numbers in ascending order. This problem has been used as a test case for functional programming.
(Full article...)
Image 8

Equilateral form of the Cairo tiling

In geometry, a Cairo pentagonal tiling is a tessellation of the Euclidean plane by congruent convex pentagons, formed by overlaying two tessellations of the plane by hexagons and named for its use as a paving design in Cairo. It is also called MacMahon's net after Percy Alexander MacMahon, who depicted it in his 1921 publication New Mathematical Pastimes. John Horton Conway called it a 4-fold pentille.

Infinitely many different pentagons can form this pattern, belonging to two of the 15 families of convex pentagons that can tile the plane. Their tilings have varying symmetries; all are face-symmetric. One particular form of the tiling, dual to the snub square tiling, has tiles with the minimum possible perimeter among all pentagonal tilings. Another, overlaying two flattened tilings by regular hexagons, is the form used in Cairo and has the property that every edge is collinear with infinitely many other edges. (Full article...)
$Image 9 Graphical demonstration of the convergence of the sum 1/2 + 1/3 + 1/7 + 1/43 + ... to 1. Each row of k squares of side length 1/k has total area 1/k, and all the squares together exactly cover a larger square with area 1. Squares with side lengths 1/1807 or smaller are too small to see in the figure and are not shown. In number theory, Sylvester's sequence is an integer sequence in which each term is the product of the previous terms, plus one. Its first few terms are :2, 3, 7, 43, 1807, 3263443, 10650056950807, 113423713055421844361000443 (sequence A000058 in the OEIS). Sylvester's sequence is named after James Joseph Sylvester, who first investigated it in 1880. Its values grow doubly exponentially, and the sum of its reciprocals forms a series of unit fractions that converges to 1 more rapidly than any other series of unit fractions. The recurrence by which it is defined allows the numbers in the sequence to be factored more easily than other numbers of the same magnitude, but, due to the rapid growth of the sequence, complete prime factorizations are known only for a few of its terms. Values derived from this sequence have also been used to construct finite Egyptian fraction representations of 1, Sasakian Einstein manifolds, and hard instances for online algorithms.[1] (Full article...)$

Image 9
Graphical demonstration of the convergence of the sum 1/2 + 1/3 + 1/7 + 1/43 + ... to 1. Each row of k squares of side length 1/k has total area 1/k, and all the squares together exactly cover a larger square with area 1. Squares with side lengths 1/1807 or smaller are too small to see in the figure and are not shown.

In number theory, Sylvester's sequence is an integer sequence in which each term is the product of the previous terms, plus one. Its first few terms are
:2, 3, 7, 43, 1807, 3263443, 10650056950807, 113423713055421844361000443 (sequence A000058 in the OEIS).

Sylvester's sequence is named after James Joseph Sylvester, who first investigated it in 1880. Its values grow doubly exponentially, and the sum of its reciprocals forms a series of unit fractions that converges to 1 more rapidly than any other series of unit fractions. The recurrence by which it is defined allows the numbers in the sequence to be factored more easily than other numbers of the same magnitude, but, due to the rapid growth of the sequence, complete prime factorizations are known only for a few of its terms. Values derived from this sequence have also been used to construct finite Egyptian fraction representations of 1, Sasakian Einstein manifolds, and hard instances for online algorithms.^[1] (Full article...)
Image 10
A simplicial line arrangement (left) and a simple line arrangement (right).

In geometry, an arrangement of lines is the subdivision of the Euclidean plane formed by a finite set of lines. An arrangement consists of bounded and unbounded convex polygons, the cells of the arrangement, line segments and rays, the edges of the arrangement, and points where two or more lines cross, the vertices of the arrangement. When considered in the projective plane rather than in the Euclidean plane, every two lines cross, and an arrangement is the projective dual to a finite set of points. Arrangements of lines have also been considered in the hyperbolic plane, and generalized to pseudolines, curves that have similar topological properties to lines. The initial study of arrangements has been attributed to an 1826 paper by Jakob Steiner.

An arrangement is said to be simple when at most two lines cross at each vertex, and simplicial when all cells are triangles (including the unbounded cells, as subsets of the projective plane). There are three known infinite families of simplicial arrangements, as well as many sporadic simplicial arrangements that do not fit into any known family. Arrangements have also been considered for infinite but locally finite systems of lines. Certain infinite arrangements of parallel lines can form simplicial arrangements, and one way of constructing the aperiodic Penrose tiling involves finding the dual graph of an arrangement of lines forming five parallel subsets. (Full article...)
Image 11
17 indivisible camels

The 17-animal inheritance puzzle is a mathematical puzzle involving unequal but fair allocation of indivisible goods, usually stated in terms of inheritance of a number of large animals (17 camels, 17 horses, 17 elephants, etc.) which must be divided in some stated proportion among a number of beneficiaries. It is a common example of an apportionment problem.

Despite often being framed as a puzzle, it is more an anecdote about a curious calculation than a problem with a clear mathematical solution. Beyond recreational mathematics and mathematics education, the story has been repeated as a parable with varied metaphorical meanings. (Full article...)
Image 12
Kissing circles. Given three mutually tangent circles (black), there are, in general, two possible answers (red) as to what radius a fourth tangent circle can have.

In geometry, Descartes' theorem states that for every four kissing, or mutually tangent circles, the radii of the circles satisfy a certain quadratic equation. By solving this equation, one can construct a fourth circle tangent to three given, mutually tangent circles. The theorem is named after René Descartes, who stated it in 1643.

Frederick Soddy's 1936 poem The Kiss Precise summarizes the theorem in terms of the bends (signed inverse radii) of the four circles: (Full article...)

Did you know

... that Fathimath Dheema Ali is the first Olympic qualifier from the Maldives?
... that Ewa Ligocka cooked another mathematician's goose?
... that Ukrainian baritone Danylo Matviienko, who holds a master's degree in mathematics, appeared as Demetrius in Britten's opera A Midsummer Night's Dream at the Oper Frankfurt?
... that Fairleigh Dickinson's upset victory over Purdue was the biggest upset in terms of point spread in NCAA tournament history, with Purdue being a 23+1⁄2-point favorite?
... that The Math Myth advocates for American high schools to stop requiring advanced algebra?
... that Latvian-Soviet artist Karlis Johansons exhibited a skeletal tensegrity form of the Schönhardt polyhedron seven years before Erich Schönhardt's 1928 paper on its mathematics?
... that the British National Hospital Service Reserve trained volunteers to carry out first aid in the aftermath of a nuclear or chemical attack?
... that circle packings in the form of a Doyle spiral were used to model plant growth long before their mathematical investigation by Doyle?

Did you know...

...that as of April 2010 only 35 even numbers have been found that are not the sum of two primes which are each in a Twin Primes pair? ref
...the Piphilology record (memorizing digits of Pi) is 70000 as of Mar 2015?
...that people are significantly slower to identify the parity of zero than other whole numbers, regardless of age, language spoken, or whether the symbol or word for zero is used?
...that Auction theory was successfully used in 1994 to sell FCC airwave spectrum, in a financial application of game theory?
...properties of Pascal's triangle have application in many fields of mathematics including combinatorics, algebra, calculus and geometry?
...work in artificial intelligence makes use of swarm intelligence, which has foundations in the behavioral examples found in nature of ants, birds, bees, and fish among others?
...that statistical properties dictated by Benford's Law are used in auditing of financial accounts as one means of detecting fraud?

More did you know facts

Showing 7 items out of 75

Featured pictures

Image 1Mandelbrot set, step 9, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 2Mandelbrot set, step 1, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 3Mandelbrot set, start, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 4Line integral of scalar field, by Lucas V. Barbosa (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 5Mandelbrot set, step 4, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 6Lorenz attractor at Chaos theory, by Wikimol (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 7Mandelbrot set, by Simpsons contributor (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 8Mandelbrot set, step 5, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 9Mandelbulb, by Ondřej Karlík (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 10Mandelbrot set, step 11, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 11Helicatenoid, by Wickerprints (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 12Hypotrochoid, by Sam Derbyshire (edited by Anevrisme and Perhelion) (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 13Mandelbrot set, step 8, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 14Missing square puzzle, by Fibonacci (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 15Radian, by Lucas V. Barbosa (from Wikipedia:Featured pictures/Sciences/Mathematics)
$Image 16Lyapunov fractal, by BernardH (from Wikipedia:Featured pictures/Sciences/Mathematics)$

Image 16Lyapunov fractal, by BernardH (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 17Mandelbrot set, step 7, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 18Mandelbrot set, step 13, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 19Mandelbrot set, step 3, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 20Mandelbrot set, step 10, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 21Fields Medal, front, by Stefan Zachow (edited by King of Hearts) (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 22Fields Medal, back, by Stefan Zachow (edited by King of Hearts) (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 23Topological knots, by Jkasd (from Wikipedia:Featured pictures/Sciences/Mathematics)
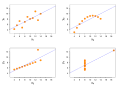
Image 24Anscombe's quartet, by Schutz (edited by Avenue) (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 25Non-uniform rational B-spline, by Greg L (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 26Mandelbrot set, step 6, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 27Breeder, by Protious/Hyperdeath (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 28Mandelbrot set, step 12, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 29Mandelbrot set, step 14, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 30Desargues' theorem, by Dynablast (edited by Jujutacular and Julia W) (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 31Cellular automata at Reflector (cellular automaton), by Simpsons contributor (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 32Mandelbrot set, step 2, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 33Tetrahedral group at Symmetry group, by Debivort (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 34Proof of the Pythagorean theorem, by Joaquim Alves Gaspar (from Wikipedia:Featured pictures/Sciences/Mathematics)

Get involved

For editor resources and to collaborate with other editors on improving Wikipedia's Mathematics-related articles, visit WikiProject Mathematics.

Categories

» Category:Mathematics, Category:People

Topics

» Lists of mathematics topics, Glossary of areas of mathematics, History of mathematics

Index of articles

ARTICLE INDEX:	0–9 A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
MATHEMATICIANS:	A B C D E F G H I J K L M N O P Q R S T U V W X Y Z

Vital articles

» subpages: Level 4 Mathematics articles, Level 5 Mathematics articles

Discover Wikipedia using portals

^ Galambos & Woeginger (1995); Brown (1979); Liang (1980).

[FOOTNOTEGalambosWoeginger1995Brown1979Liang1980-1] Galambos & Woeginger (1995); Brown (1979); Liang (1980).

[1]